Types of Regression Analysis in Machine Learning
Learn what is regression analysis and understand the different types of regression analysis techniques in machine learning.

Regression analysis is the favorite of data science and machine learning practitioners as it provides a great level of flexibility and reliability making it an ideal choice for analyzing different situations like -
Do educational degrees and IQ affect salary?
Is consuming caffeine and smoking-related to mortality risk?
Do regular workouts and a dietary plan affect weight?
Time Series Project to Build a Multiple Linear Regression Model
Downloadable solution code | Explanatory videos | Tech Support
Start ProjectTable of Contents
- What is Regression Analysis?
- Regression Analysis: Understanding the Related Terminology
- 15 Types of Regression Analysis in Machine Learning
- 1) Linear Regression Analysis:
- 2) Polynomial Regression Analysis
- 3) Logistic Regression Analysis
- 4) Quantile Regression Analysis
- 5) Ordinal Regression Analysis
- 6) Support Vector Regression
- 7) Poisson Regression Analysis
- 8) Negative Binomial Regression:
- 9) Principal Components Regression:
- 10) Partial Least Squares Regression
- 11) Tobit Regression Analysis
- 12) Cox Regression Analysis
- 13) Ridge Regression Analysis
- 14) Lasso Regression
- 15) ElasticNet Regression
- Choose the Right Type of Regression Analysis Model for Machine Learning
- Regression Analysis Machine Learning Projects
What is Regression Analysis?
According to Wikipedia, Regression Analysis is defined as a set of statistical processes for estimating the relationship between a dependent variable and one or more independent variables.
Didn’t make much sense, did it?
Let's try to understand regression analysis with an example. Imagine you have made plans with friends after a long time and you wish to go out, but you are not sure whether it will rain or not. It’s the monsoon season, but your mom says the air feels dry today, and therefore the probability of raining today is less. On the contrary, your sister believes because it rained yesterday it’s likely that it will rain today. Considering you are no Lord of Thunder and you have no control over the weather, how will you decide whose opinion to take more seriously, keeping in mind the fact that you are impartial towards both?
Regression Analysis might come to your rescue. There are many factors on which rain depends like geography, time of the year, precipitation, wind speed but unless you are the weather department or Sheldon you wouldn’t want to work with all these values.

Image Source: memegenerator.net
So, you would take the humidity level and the previous day’s precipitation to decide today’s level of precipitation level(or the amount of rainfall). You can get both of these values easily on the internet, I know you can get the weather forecast for today too, but we are trying to learn something here.
In our example what we are trying to predict is today’s precipitation level which is dependent on the level of humidity and rain received yesterday hence it is called, the dependent variable. The variables on which it depends will be called independent variables. What we try to do with regression Analysis is to model or quantify the relationship between these two kinds of variables and hence predict one with the help of the other with a level of certainty. An informed guess is better than random guessing, right? To solve our problem If we were to do a simple linear regression, we would collect the humidity level and precipitation level for the previous month and plot them.
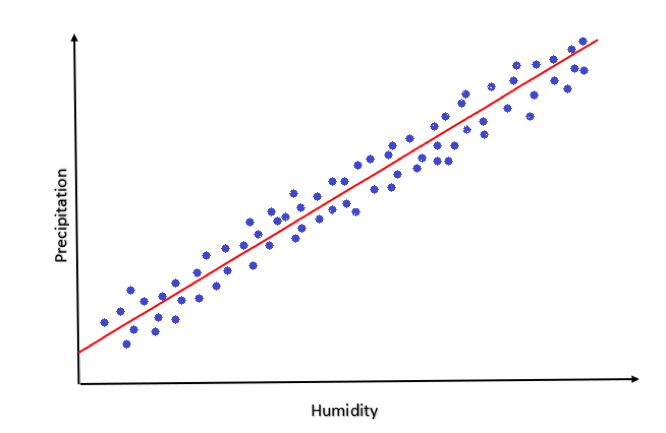
Even without doing any math, we can infer that humidity and rainfall(precipitation) are linearly correlated. An increase in the value of one leads to an increase in the other value too. But here you can see we have oversimplified the problem by making a lot of assumptions, the major one being humidity is the only or the most important factor in deciding rainfall. In real-world (not-so simplified) business problems, there are many variables with complex relationships between them. To deal with all such complexities, there are several different types of regression analysis methods out there and we’ll be looking at each one closely in this article.
New Projects
Regression Analysis: Understanding the Related Terminology
But before we go any further, let’s look at some of the most common terminologies associated with regression analysis that will come up:

- Outliers: Outliers are basically values or data points that are very stray from the general population or distribution of data. Outliers have the ability to skew the results of any ML model towards their detection. Therefore, it is necessary to detect them early on or use algorithms resistant to outliers.
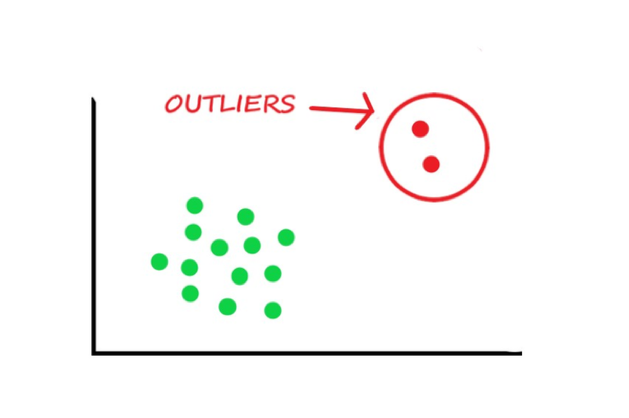
Image Source: https://datascience.foundation/
Here's what valued users are saying about ProjectPro

Ameeruddin Mohammed
ETL (Abintio) developer at IBM

Gautam Vermani
Data Consultant at Confidential
Not sure what you are looking for?
View All Projects- Overfitting: Overfitting happens when the ML model learns the training data such that it memorizes every little detail and noise, making it less generalizable and therefore the model performs badly on any unknown dataset and is ridiculously complex.

Image Source: https://towardsdatascience.com/
- Heteroscedasticity: This term is hard to even read, let alone to understand. So, we’ll take an example. We have humidity which predicts rainfall or precipitation. Now as humidity increases the amount by which precipitation increases or decreases is variable and is not fixed. If the level of precipitation would have increased/decreased constantly as the humidity was increasing, we would have called it homoscedasticity.
15 Types of Regression Analysis in Machine Learning

1) Linear Regression Analysis:
The type of regression we observed above is linear regression. There is assumed to be a linear relationship between the variable we want to predict and the explanatory variable. Linear regression will attempt to model the relationship between two variables by fitting a linear equation to the observed data. In our case, y is the level of precipitation and X is humidity, while a and b are regression coefficients. For all the observed points y, X we try to find the values of a and b that best fit our equation. In a little complex scenario, there would be a lot of variables affecting rain like temperature, day of the year, amount of precipitation the previous day, etc. For such cases with more than one independent variable, we have multiple linear regression and the equation for it goes like this -
y = a + bX + cX2 + dX3 …….
where X1, X2, X3 are all explanatory variables and a, b, c are regression coefficients. A positive coefficient tells how much of a positive influence a predictor has on the dependent variable and a negative coefficient says vice versa.
Get Closer To Your Dream of Becoming a Data Scientist with 70+ Solved End-to-End ML Projects
Benefits and Applications of Linear Regression Analysis
-
Despite being so simple Linear Regression is a very powerful technique that can be used to generate insights on consumer behavior, understanding business and factors influencing profitability. It can be used in business to evaluate trends and make estimates or forecasts.
- Linear regression can also increase the operational efficiency of the business by data-driven decision-making. A bike rental company can avoid overstocking or understocking of bikes by modeling the relationship between the number of bikes rented and factors like time of the day, traffic on the road, weather, etc.
Limitations and Assumptions of Linear Regression Analysis
- Linear regression assumes a linear relationship between the dependent and independent variables which is often not the case in real-world scenarios. This is when you would want to go with other regression techniques that account for non-linearity.
- Linear Regression also won’t do well if the independent variables are related to each other, in other terms if there is Multicollinearity. To avoid this, only keep one of the correlated independent variables.
- It also assumes different observations are independent of each other. Today’s rainfall is independent of yesterday’s rainfall, which again is not a very realistic assumption.
Free access to solved Python regression analysis code examples can be found here (these are ready-to-use for your ML projects)
2) Polynomial Regression Analysis
The need for polynomial regression stems from the need to model relationships between the dependent and independent variables when it’s non-linear, which is often the case in most practical applications. The equation for polynomial regression would obviously be a multinomial one:
y = a + bX + cX2 + dX3 ……
Before we go any further, let me introduce a concept called loss function, used to assess the usefulness of our regression algorithm. While fitting our regression line to our data, we position the line in such a way that the sum of perpendicular distances of the data points from the line is minimized.

The Root Mean Squared error is very similar to this, it just takes the square of these residuals(the distance of a point from the line) and takes a root of their sum.

Here Predictedi are the red points and Actualiare the black points. RMSE will tell you how well fit the line of regression is.
Now, coming back to polynomial regression, when the relationship between variables is not linear, it’s hard to fit a line on the data and minimize our cost function. This is when we need Polynomial Regression.

Benefits and Applications of Polynomial Regression Analysis
- Besides providing the best level of approximation between the variables, polynomial regression also provides a broad range of functions that can fall under its hood.
- In industry, polynomial regression can be used for all cases where linear regression is used but with a greater degree of reliability, since we are not violating the linearity assumption.
Limitations and Assumptions of Polynomial Regression Analysis
- Most of the assumptions made for linear regression are still valid here. It is assumed that the data is not multicollinear, independent of subsequent observations, and no Heteroscedasticity.
- Polynomial Regression is also sensitive to the presence of outliers. It’s also hard to detect outliers with an algorithm and their presence skews the result in their direction.
3) Logistic Regression Analysis
A common feature in the above two methods was the dependent variable was continuous, in Logistic Regression the dependent variable is discrete(or categorical) while the independent variables could be discrete or continuous. It is named after the function at its core called the Logarithmic function. The equation goes like this:

Where x1, x2,x3 are independent variables and b0, b1, b2 are regression coefficients. In a Binary Classification problem, p gives the probability that the sample belongs to the main class.
When Logistic regression is applied in real-world problems – like detecting cancer in people P here, would tell the probability of whether the person has cancer or not. P less than 0.5 would be mapped to no cancer and greater than that would map to cancer. Logistic regression is a linear method, but the predictions are transformed using the logistic function. The curve for it follows the curve for log function.

Implement end-to-end ML Projects using Logistic Regression
Benefits and Applications of Logistic Regression Analysis
- Logistic Regression is one of the most widely used algorithms out there. It is easy to implement and versatile. From petal recognition to text classification, it is used on top(as a classification layer) of some of the most sophisticated deep Learning architectures out there.
- It can be used with a variety of output classes and it also outputs the magnitude of association with a class. It can also interpret model coefficients as indicators of feature importance.
- Unlike other classification algorithms like SVM, it is relatively faster to train.
Limitations and Assumptions of Logistic Regression Analysis
-
Logistic Regression is at the core of a linear algorithm; thus, it follows most of the assumptions of linear regression like the linear relationships between the input variables and output variables, auto-correlation, etc.
-
Logistic Regression can overfit if the number of observations is less than the number of independent variables.
-
It is also sensitive to outliers and noise in the data.
Free access to solved code Python and R examples can be found here (these are ready-to-use for your Data Science and ML projects)
4) Quantile Regression Analysis
In probability distributions, quantiles are points dividing the range of distributions into continuous intervals with equal probabilities. For a normal distribution the quantiles would be placed as follows :

In our probability distribution, 25% of the data points would lie on the left of Q1 and 75% would lie to the left of Q3.
Ordinary Least Squares Regression or Linear Regression is modeled around the mean of the dependent variable. Quantile regression allows us to understand relationships between variables outside of the mean of the data, making it useful in understanding outcomes that are non-normally distributed and that have non-linear relationships with predictor variables. The equation for the ðœth quantile is given by

Where ðœ could be the first, second, or third quantile. p is the number of dependent variables and all the βs are regression coefficients that we model.
Benefits and Applications of Quantile Regression Analysis
-
Quantile regression can be used when the assumptions of linear regression are not met. It is robust to outliers and can be used when heteroscedasticity is present.
- It is also useful when data is skewed as it does not depend on measures of mean but quantiles. In any business, it is likely that the amount of money spent by customers is skewed and the business might be more interested in the top quantiles rather than the mean.
Limitations and Assumptions of Quantile Regression Analysis
-
If all assumptions of the Linear Regression model are met, Quantile Regression is less efficient than the alternative.
- Unlike Logistic Regression, Quantile Regression works on predicting continuous variables and does so less precisely since it makes predictions over quantiles.
Get Closer To Your Dream of Becoming a Data Scientist with 70+ Solved End-to-End ML Projects
5) Ordinal Regression Analysis
When the dependent variables are ordinal, this technique is used. Ordinal variables are categorical variables, but the categories are ordered/ranked like Low, Moderate, High. Ordinal Regression can be seen as an intermediate problem between regression and classification. The formula for Ordinal Regression comes from a technique called Generalized Linear Model and goes as follows:
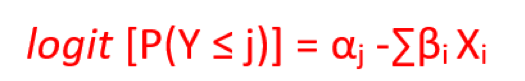
Benefits and Applications of Ordinal Regression Analysis
-
Ordinal regression turns up often in the social sciences, for example in the modeling of human levels of preference (on a scale from, say, 1–5 for "very poor" through "excellent"), as well as in information retrieval.
-
It serves as the best technique for predicting multiclass ordered variables.
Limitations and Assumptions of Ordinal Regression Analysis
-
Parallel lines assumption: There is one regression equation for each category except the last category. The last category probability can be predicted as a 1-second last category probability.
- Estimates are sometimes implausible, suggesting that the data are being spread too thin and another method is needed.
Free access to solved Python regression analysis code examples can be found here (these are ready-to-use for your ML projects)
6) Support Vector Regression
Before we go any further with this, let me explain the concept of Support Vector Machines(SVM). Let’s take an example of a 2D dataset having 2 features(independent variables) and 2 classes. We can easily plot them into a 2D space.
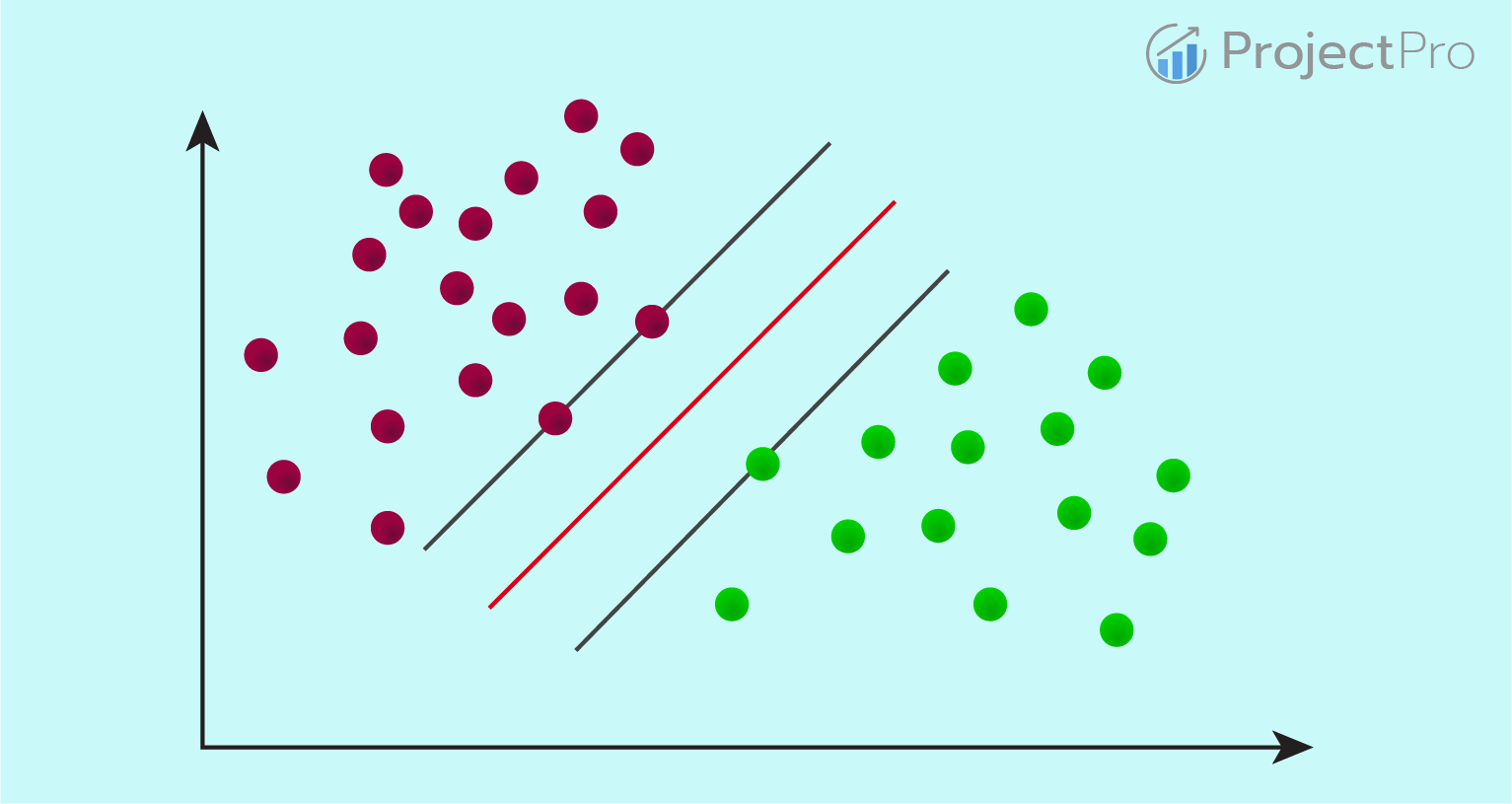
The red dots correspond to one class and green to the other. These classes can be easily separated by a line in 2D space. But for SVM, it can’t be just any line. The distance between the points in the two classes closest to each other is taken and the line passing mid-way through it is the optimal dividing plane. These points that play a major role in deciding the position of the separator line are called Support Vectors and hence the whole technique is called Support Vector Machine. In more realistic cases, we have an n-dimensional space, where n is the number of features and the decision plane is obviously not linear.
In Support Vector Regression, instead of having a discrete dependent variable, we have a continuous one and instead of having a decision boundary, we have a regressor line to fit our data. Now, the way we find the best fit line or plane is a little different from what we did above. Again, for the purpose of simplification consider a 2D plane.

The points are distributed in the 2D space. Now the two points farthest from each other, in other words having the maximum distance between them are the support vectors and the line passing through the median of that perpendicular distance is our best-fit line.
Benefits and Applications of Support Vector Regression Analysis
-
While being robust to outliers, SVR works way better in high-dimensional space than the linear regression model.
-
You can define a confidence interval or level of tolerance, marked by C while training. The prediction accuracy is improved by measuring confidence in classification. This is useful in real-world systems that do not require a very precise prediction, but a prediction between a confidence interval.
- It is very easy to accommodate new data points in support vector regression analysis.
Limitations and Assumptions of Support Vector Regression Analysis
-
They take a lot of time to train and are not suitable for larger datasets.
-
SVR will seriously underperform if the number of samples is less than the number of features. There are no probabilistic explanations for the predictions.
7) Poisson Regression Analysis
Poisson distribution is a discrete probability distribution covering the number of events occurring in a period of time, given the average number of times that event has occurred in that period. When the dependent variable follows Poisson distribution or is count-based, we use Poisson Regression. Count-based data contains events that occur at a certain rate. The rate of occurrence may change over time or from one observation to the next. The instance we stated above is an example of this. The formula for Poisson distribution follows this probability mass function:

Where PX(k) is the probability of seeing k events in time t, e-(λt) is the event rate or the number of events happening per unit time and k is the number of events.
Consider a small-scale restaurant where we are recording the number of customers walking in an hour between 10 a.m. – 11 a.m., on average 5 customers are in the restaurant at this hour. With this information, we can calculate the probability that there will be no customer between 10 a.m. – 11 a.m. as follows:
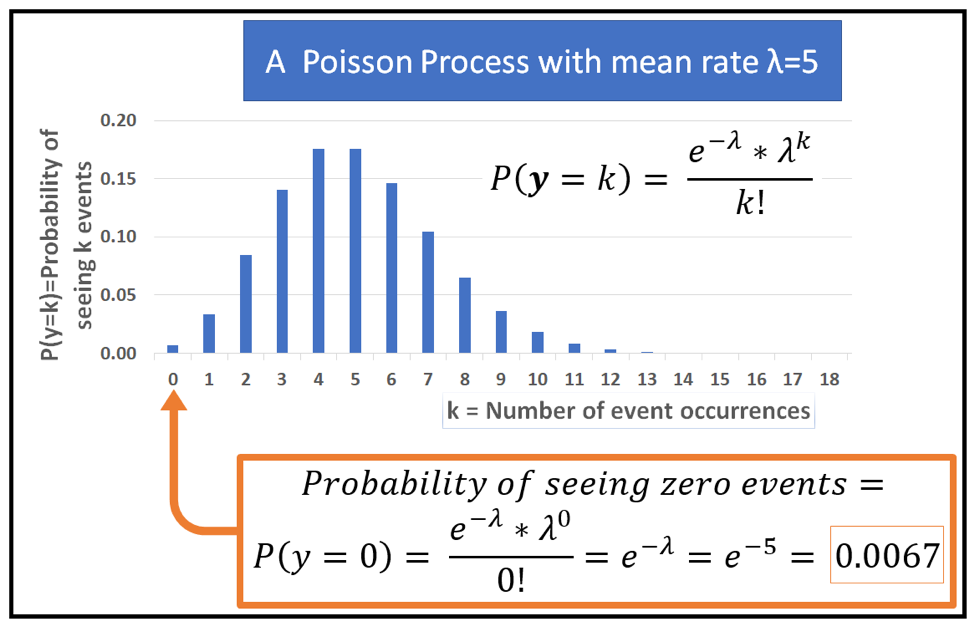
Image Source: https://towardsdatascience.com/
Benefits and Applications of Poisson Regression Analysis
-
A lot of businesses rely on count-based data like the number of bikes rented in an hour, the number of calls received in a call center at a particular time in the day, or the number of pizzas ordered during a particular time in the month.
- It is useful when the data is skewed and sparse.
- It is used to determine the probable maximum and the minimum number of times the event will occur within the specified time frame.
Limitations and Assumptions of Poisson Regression Analysis​
- The assumption of Poisson Regression is that the dependent variable must be count-based, the observations must be independent of another and the mean of the Poisson random variable must be equal to its variance.
- Poisson regression may not perform well in situations where the conditional variance is greater than the conditional mean, a phenomenon known as overdispersion.
Recommended Reading:
8) Negative Binomial Regression:
Like Poisson Regression, Negative Binomial Regression also works on count data. In a way, Negative Binomial Regression is better than Poisson distribution because it doesn’t make the mean equal to the variance assumption. This strict assumption is often not satisfied by real-world data. In real-world data, the variance is either greater than the mean called overdispersion or less than the mean called under-dispersion.
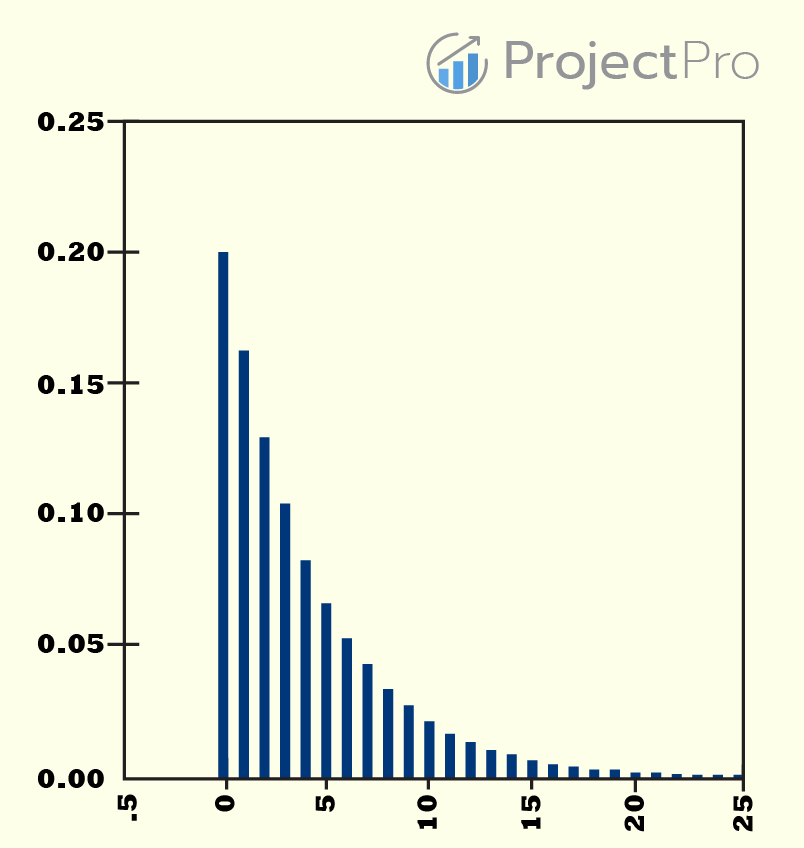
The plot is pretty much the same as Poisson Distribution. Negative Binomial Regression can be considered as a generalization of Poisson regression since it has the same mean structure as Poisson regression, and it has an extra parameter to model the over-dispersion.
Benefits and Applications of Negative Binomial Regression Analysis
-
A use case for this would be School administrators study the attendance behavior of high school juniors at two schools. Predictors of the number of days of absence include the type of program in which the student is enrolled and how well he/she does in a standardized test in math.
- It has a clear advantage over Poisson Regression since it does not make the mean equal to variance assumption.
Limitations and Assumptions of Negative Binomial Regression Analysis
-
When the number of samples is small, negative binomial regression may not be a good choice.
- The outcome variable cannot have negative numbers.
9) Principal Components Regression:
This regression technique is based on Principal Component Analysis. In PCR, instead of regressing the dependent variable on the explanatory variables directly, the principal components of the explanatory variables are used as regressors. Let’s see what’s PCA first. PCA is basically a dimensionality-reduction method that is used to reduce the dimensionality (number of features) of large datasets without losing most of the information. A little accuracy is traded for simplicity.
Here’s an example of converting the points from 2D to 1D space.

In PCR, the steps followed are as follows:
- Perform PCA on the explanatory variables to obtain principal components and then choose a subset from this.
- Using this subset and our dependent variable, fit a linear regression model to get a vector of estimated regression coefficients.
- Transform this vector back to the scale of the original independent variables.
Benefits and Applications of Principal Component Regression Analysis
-
One of the greatest advantages of PCR is the consistency check that one gets on the raw data, which you don’t have for MLR. PCR is also way less prone to overfitting.
- PCR can be used even when the explanatory variables are correlated. It can also be run when there are more features than observations.
Limitations and Assumptions of Principal Component Regression Analysis
-
One of the biggest disadvantages of PCR is, that it does not consider the dependent variable when deciding which principal components to drop. The decision to drop components is based only on the magnitude of the variance of the components.
- In PCA data is not normalized, so it’s sensitive to the scale of features. Changing the scale would completely change the results of PCA.
Get More Practice, More Data Science and Machine Learning Projects, and More guidance.Fast-Track Your Career Transition with ProjectPro
10) Partial Least Squares Regression
It is an extension of Principal Components Regression. Instead of finding hyperplanes of maximum variance between the dependent and independent variables, it finds a linear regression model by projecting the predicted variables and the observable variables to a new space. Both kinds of variables are mapped into a new space, hence it overcomes a limitation of PCA. A PLS regression model will try to find the multidimensional direction in the X space that explains the maximum multidimensional variance direction in the Y space. The mathematical model is given by:
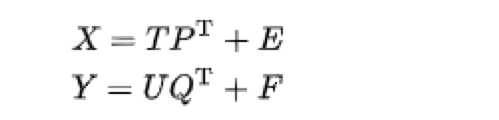
where X is a matrix of independent variables, Y is a matrix of dependent variables; T and U matrices that are, respectively, projections of X and projections of Y, P, and Q are, respectively orthogonal loading matrices; and matrices E and F are the error terms, which are independent and identically distributed random normal variables. The decompositions of X and Y are to maximize the covariance between T and U.
Benefits and Applications of Partial Least Squares Regression
-
PLS can be used for the detection of outliers. Like PCR, it can also handle more features than observations.
- It also provides more predictive accuracy and a lower risk of finding correlation on chance. It has most of the same benefits as PCR.
Limitations and Assumptions of Partial Least Squares Regression
-
The major limitations are a higher risk of overlooking real correlations and sensitivity to the relative scaling of the descriptor(independent) variables.
- This technique is again sensitive to scaling.
11) Tobit Regression Analysis
In Tobit Regression, the observed or known range of the dependent variable is censored in some way. In statistics, censoring is a condition in which the value of a variable is only partially known. Censoring or clipping can occur in the following ways- Censoring from above takes place when cases with a value at or above some threshold, all take on the value of that threshold so that the true value might be equal to the threshold, but it might also be higher. In the case of censoring from below, values those that fall at or below some threshold are censored.
Let’s look at an example of Tobit analysis-
A research project is studying the level of lead in home drinking water as a function of the age of a house and family income. The water testing kit cannot detect lead concentrations below 5 parts per billion (ppb). The EPA considers levels above 15 ppb to be dangerous. These data are an example of left-censoring (censoring from below). You can refer to this excellent blog to read more about Tobit Regression Analysis
Benefits and Applications of Tobit Regression Analysis
-
Tobit's method can be easily extended to handle truncated and other non-randomly selected samples. Tobit models have been applied in demand analysis to accommodate observations with zero expenditures on some goods.
- It has also been applied to estimate factors that impact grant receipt, including financial transfers distributed to sub-national governments who may apply for these grants. In these cases, grant recipients cannot receive negative amounts, and the data is thus left-censored.
Limitations and Assumptions of Tobit Regression Analysis
-
One limitation of the Tobit model is its assumption that the processes in both regimes of the outcome are equal up to a constant of proportionality.
- If you have a fundamentally bounded dependent variable rather than a truncated one you might want to move to a generalized linear model framework with one of the (less often chosen) distributions for Y e.g. log-normal, gamma, exponential, etc. which respect that lower bound.
12) Cox Regression Analysis
The Cox regression model is commonly used in medical research for studying the association between the survival time of patients and one or more predictor variables(values on which survival time is dependent). The purpose of the model is to evaluate simultaneously the effect of several factors on survival. In other words, it allows us to examine how specified factors influence the rate of a particular event happening (e.g., infection, death) at a particular point in time. This rate is commonly referred to as the hazard rate. Predictor variables (or factors) are usually termed covariates in the survival-analysis literature. The Cox model is expressed by the hazard function denoted by h(t). Briefly, the hazard function can be interpreted as the risk of dying at time t. It can be estimated as follow:​

t stands for survival time, h(t) is the hazard function, the coefficients b1, b2,…etc measure the impact of covariates x1, x2 , …xp . The term h0 is the baseline hazard.
Benefits and Applications of Cox Regression Analysis
-
It can be used in investigating the impact of diet, amount of exercise, hours of sleep, age on the survival time after a person has been diagnosed with a disease such as cancer. Survival data usually has censored data and the distribution is highly skewed. Because of these two problems, Multiple Regression cannot be used.
- It uses a multivariate approach and can account for the impact of each variable on the outcome.
Limitations and Applications of Cox Regression Analysis
-
If the proportionality of the hazard assumption is not met, the outcome of regression is incorrect.
- The model also assumes that each covariate has a multiplicative effect in the hazards function that is constant over time.
13) Ridge Regression Analysis
Before going any further with this let’s understand the concept of regularization. Regularization is a technique used to deal with overfitting. It adds an additional error term to the loss function that penalizes overfitting and promotes generalization. So, in addition to optimizing the model coefficients for loss, we also optimize for the regularization term, so we get a well-fit model. There are basically 2 kinds of regularizations – L1 and L2. We’ll better understand them as we’ll go through the regression models that use them. Ridge Regression uses L2 regularization also called the L2 penalty which is the square of the magnitude of model coefficients added to the error term. It is merely an extension of simple linear regression model with better control on overfitting. The ridge regression model equation remains the same as in multiple linear regression:
y = a + bX + cX2 + dX3 …….
If the loss function we have chosen is RMSE:

Then now the error becomes:
Error = RMSE + λ (a2 + b2 + c2 +………)
Here, λ is the level of regularization.
Benefits and Applications of Ridge Regression Analysis
-
Deals with overfitting, make the model generalize well.
- Shrinks model coefficients and reduce the model complexity and multi-collinearity. In any real-world scenario, Ridge Regression is always a better method than Linear Regression because of its ability to learn general patterns rather than noise.
Limitations and Assumptions of Ridge Regression Analysis
-
Ridge Regression is at the heart of a linear regression model and thus can only be used to model linear relations. It makes most assumptions of the linear regression model.
- Doesn’t deal well with sparse data like the regression technique I’ll describe next.
14) Lasso Regression
Lasso is also an extension of Linear Regression, but it implements L1 regularization instead of L2. The only difference between L1 and L2 is instead of taking the square of the coefficients, magnitudes are taken into account.
The error term now is:
Error = RMSE + λ(|a| +| b| +| c| +………)
Here, λ is used to control the level of regularization. The goal of lasso regression is to obtain the subset of predictors that minimizes prediction error for a quantitative response(dependent) variable. It does this by imposing a constraint on the model parameters that causes regression coefficients for some variables to shrink toward zero. Variables with a regression coefficient equal to zero after the shrinkage process are excluded from the model. Variables with non-zero regression coefficients variables are most strongly associated with the response variable. Thus, it helps in feature selection.
Benefits and Applications of Lasso Regression Analysis
-
It avoids overfitting and can be used when the number of features is more than the number of samples. Lasso regression is well suited for building forecasting models when the number of potential covariates is large, and the number of observations is small or roughly equal to the number of covariates.
- It does feature selection and reduces model complexity through it. It’s also fast, in terms of training and inference on test data.
Limitations and Assumptions of Lasso Regression Analysis
-
Since it’s a linear model at the core, it follows most of the assumptions of a linear model. It also fails to do grouped selection. It tends to select one variable from a group and ignore the others.
- It’s not very intuitive, in the sense that there is no way to know why it selected the features it did. It might lose some important independent variable on the way, but this is dependent on the level of regularization λ.
15) ElasticNet Regression
ElasticNet is a combination of Lasso and Ridge Regression in the sense that it uses both L1 and L2 regularization. The feature selection of Lasso can be too dependent on data and thus unstable, therefore ElasticNet combines the two approaches to give the best of both worlds.
The error term goes like this :
Error = RMSE + λ α × L1 penalty+1- α ×L2 penalty
Here, λ is used to control the level of regularization as usual while α is to give weights to L1 and L2 penalty. The value always lies between 0 and 1.
Benefits and Applications of ElasticNet Regression Analysis
-
Deals with overfitting and can also do feature selection with L1 regularization.
-
Can perform grouped selection because of the presence of L2 penalty. It has interesting applications in sparse PCA and new support kernel machines.
- It is also used in Cancer prognosis and portfolio optimization.
Limitations and Assumptions of ElasticNet Regression Analysis
-
Regularization leads to dimensionality reduction, which means the machine learning model is built using a lower-dimensional dataset. This generally leads to a high bias error.
- Again, it follows all the assumptions of a linear model.
Choose the Right Type of Regression Analysis Model for Machine Learning
As we already know, there are a variety of regression analysis techniques and the one you choose would depend on several factors like:
- The type of dependent variables- continuous, discrete, count-based, or time-based.
- The amount of generalization you need in your model.
- The kind of assumptions you can work with- there’ll be a tradeoff between the number of assumptions and the accuracy of the model on real-world data.
- Whether your data is skewed or has outliers.
- If there is a relationship between your independent variables.
- The kind of relationship between your predictors and outcome – linear/non-linear.
So, choose one wisely!
Regression Analysis Machine Learning Projects
Now, it's time to put the regressional analysis techniques learned in this article to put into practice. Master real-world regression analysis techniques with access to 50+ solved end-to-end data science and machine learning projects curated just for you. ProjectPro lets you experiment with these regression models in machine learning through real-world datasets. Here are some machine learning projects that use the popular regression analysis methods -
Big Mart Sales Prediction Machine Learning Project for Beginners
Insurance Pricing Forecast using Regression Analysis
ML Project on Churn Prediction using Logistic Regression Analysis
About the Author
ProjectPro
ProjectPro is the only online platform designed to help professionals gain practical, hands-on experience in big data, data engineering, data science, and machine learning related technologies. Having over 270+ reusable project templates in data science and big data with step-by-step walkthroughs,



