Support Vector Machine (SVM)
In data analytics or decision sciences most of the time we come across the situations where we need to classify our data based on a certain dependent variable. To support the solution for this need there are multiple techniques which can be applied; Logistic Regression, Random Forest Algorithm, Bayesian Algorithm are a few to name. SVM is a machine learning technique to separate data which tries to maximize the gap between the categories (a.k.a Margin).
Maximum Margin Classifier:
Maximum Margin Classifier is the simple way to divide your data if your data if your data is linearly (or via a plane in multi-dimensional space) separable. But due to obvious reasons it can’t be applied to the data where no clear linear boundary is possible.
Support Vector Classifier:
SVC is an extension to maximum margin classifier where we allow some misclassification to happen.
Support Vector Machine:
Support Vector Machine or SVM is a further extension to SVC to accommodate non-linear boundaries. Though there is a clear distinction between various definitions but people prefer to call all of them as SVM to avoid any complications.
- Logistic Regression works when we have data which is linearly separable, e.g, following datasets are linearly separable and can be classified using any linear separating technique.

- But, What if we have data something like given in the following example? Can you see any linear separating boundary in this case?

- In the below example there is no separating boundary which can divide this data in the current dimensions (1D) but can there be any boundary which can promote the data in higher dimensions?

Maximum Margin Classifier
Before we start let’s first understand “What is Hyperplane?” In a P-Dimensional space, a hyperplane is a flat subspace having dimensions “P-1” i.e., in a 2-D space a hyperplane will be a line-
B0+B1X1+B2X2=0
While in an m-dimensional space-
B0+B1X1+B2X2+…+BmXm=0
A hyperplane divides the space into two parts –
B0+B1X1+B2X2+…+BmXm< 0, and
B0+B1X1+B2X2+…+BmXm> 0

As you can see that there can be multiple possible such hyperplanes which divide the data. Consider the following illustration for this point –

This represents a confusion state for an analyst to choose any one of them. But this is where Maximum Margin Classifier comes into picture. Maximum Margin Classifier, helps to choose the optimal solution from a set of possible solutions set. Our objective here is to identify the separating hyperplane which is farthest from the observations. If we calculate the perpendicular distance from each point in training dataset to the separating hyperplanes, our optimal solution will have the plane with maximum Margin. To simplify if we insert a slab to separate our data, the optimal solution will have the maximum width and the center line of the slab is called the hyperplane.

Get Closer To Your Dream of Becoming a Data Scientist with 70+ Solved End-to-End ML Projects
In the example shown above we can see that there are 4 points which are nearest to the boundary or are defining boundary, these points are called “Support Vectors”. Let’s try to learn the concept using a real example, we will be using “R” to run our experiment. We first need to create a dataset which we can use to classify, we will be using the following data to learn maximum margin classifier:
|
x |
Y |
Flag |
|
-1.34064 |
2.205443 |
-1 |
|
-1.05063 |
-0.49391 |
1 |
|
-1.04402 |
1.950164 |
-1 |
|
-0.75047 |
0.191654 |
1 |
|
-0.5096 |
0.865357 |
1 |
|
-0.36403 |
2.323345 |
-1 |
|
-0.35028 |
-0.16828 |
1 |
|
-0.31301 |
-0.54001 |
1 |
|
-0.24855 |
0.682347 |
1 |
|
-0.21694 |
0.034097 |
1 |
|
0.499221 |
0.834591 |
-1 |
|
0.620264 |
-0.03877 |
1 |
|
0.688669 |
1.38551 |
-1 |
|
0.713676 |
0.09454 |
1 |
|
0.772188 |
1.539164 |
-1 |
|
1.244595 |
-0.18418 |
1 |
|
1.326428 |
1.400617 |
-1 |
|
1.640474 |
1.177086 |
-1 |
|
2.335457 |
-0.4978 |
-1 |
|
2.705731 |
1.526312 |
-1 |
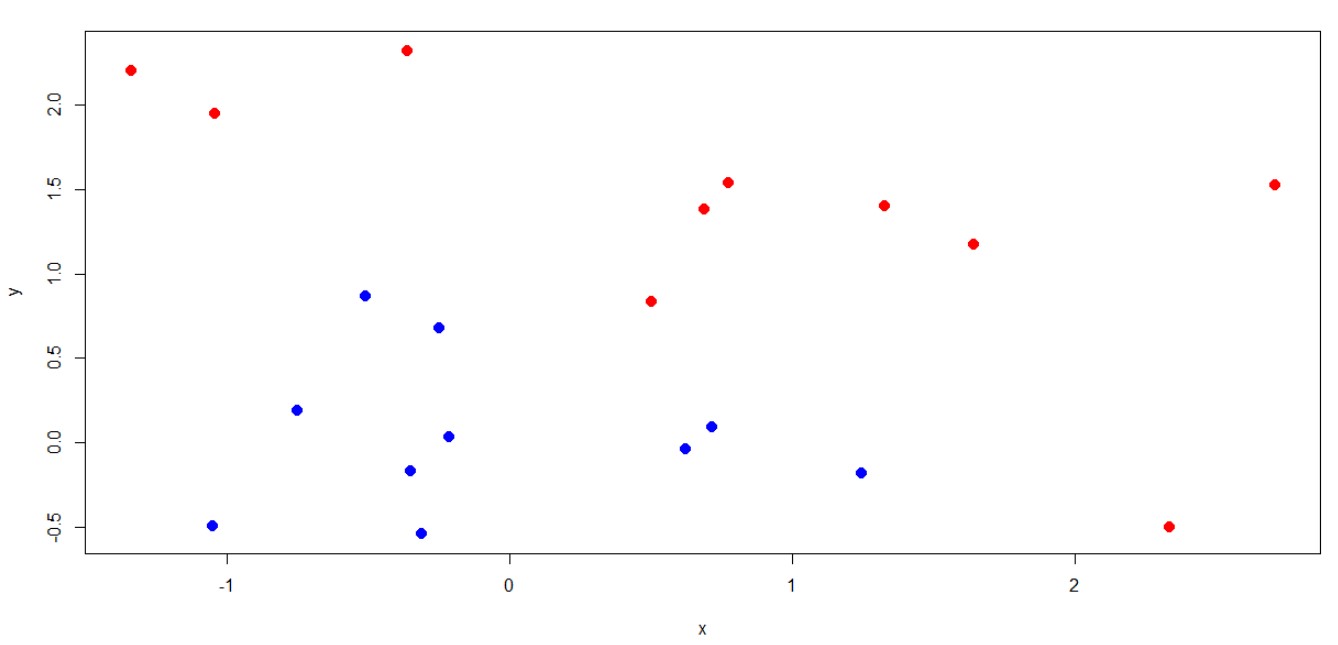
Next, we need to load R-Package to run SVM. “e1071” is the package provided by CRAN which can be used for this purpose. Once we have loaded the package next we just need to run the SVM function and fit the classification boundary.

Here, you can see that we have used “Linear” kernel to separate data because we assumed that our data is linearly separable. Next, the algorithm has used 4 data points as support vectors to create a hyperplane. This is how the classification result looks like:

Points denoted by “x” are support vectors.
Get FREE Access to Machine Learning Example Codes for Data Cleaning, Data Munging, and Data Visualization
Theory behind the MMC
As we have seen an example to see how Maximum Margin Classifier works, now let’s try to understand the maths behind it. Assuming that we have a set of ‘n’ training observations in a ‘P’ dimensional plane i.e.,
x1, … xn ϵ Rp
And, associated class labels y1, y2… , yn ϵ {-1, 1}
Finding the optimal maximum margin classifier plane is the solution to the optimization problem –
Maximize M …… (1)
Subject to, 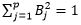
Yi (B0 + B1Xi1 + B2Xi2 + …. BpXip) >= M, i=1, 2……n ….. (3)
Constraint 3 makes sure that each observation will be on the correct side of the output hyperplane, provided ‘M’ is positive.
The Non –Separable Case
Maximum Margin Classifier is a choice when data is linearly separable but in many of the cases with no separating boundary possible and hence there is no solution with M>0. Hence, there is a need to extend the concept of a separating hyperplane in order to develop a hyperplane that ALMOST separates the classes, using so called SOFT MARGIN. This generalization is called “Support Vector Classifier”. We want a hyperplane that does not perfectly separate two classes, in the interest of
- Greater robustness to individual observation
- Better classification of most of the training observations
We allow few of the observations to be on the wrong side of the hyperplane using the solution to the following optimization problem
Maximize M …… (1)
Subject to,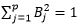
Yi (B0 + B1Xi1 + B2Xi2 + …. BpXip) >= M (1-ϵi), i=1, 2……n ….. (3)
ϵi>=0, 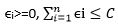
Where C is a non-negative tuning parameter. In (3) ϵi….. ϵn are slack variables that allow individual observation to be on the wrong side of margin or the hyperplane. C bounds the sum of ϵis and so determine the number and severity of violation to the margin that we will tolerate. The important point to consider here is that the observations which lies strictly on the correct side of the plane do not affect the support vector classifier. Rather, the observations that are lying directly on the margin or on the wrong side of the margin are known as support vectors.
Support Vector Machine (SVM)
Till now we were discussing the options when our data is linearly separable, either allowing some Soft Margin or without any soft Margin.
But what about the cases where our data is not linearly separable? What if there is no plane which can divide our data? E.g., consider the following images-
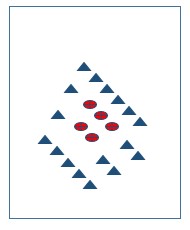
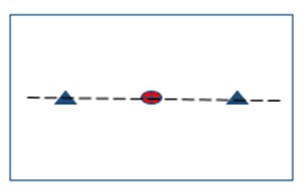
SVM is a further extension of SVC that results from enlarging the feature space in a specific way using “KERNELS”. The main idea is that we may want to enlarge our feature space in order to accommodate a non-linear boundary between the classes. For example, the right hand side image shown above is not separable in given dimensions but what if we promote it to 2-D instead of 1-D?
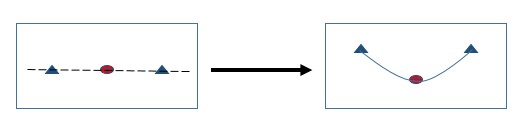
Now, you can see that there is a clear separating boundary possible; which can divide data into two classes. Dealing with high dimensional data or enlarging the feature space requires high computational power. The Kernel approach is simply an efficient computational approach for the same. Solution to the Support Vector Classifier problem involves only the inner – product of the observations and not the variables themselves. This is the basic idea behind using a Kernel technique. A Kernel is a function that quantifies the similarity of two observations, for example
K ( Xi, Xi’) = 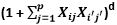
When a Support Vector Classifier is combined with a non-linear Kernel, the resulting classifier is known as SVM. SVM function in e1071 package for R has multiple other Kernels i.e., Radial, Sigmoid apart from Linear and Polynomial.

Depending on your data you have to select the Kernel which best classifies your data. There is no direct rule or formula which can tell you to choose a Kernel, most of the times it will be try and succeed method. As you can see in the Kernel explanation above, there are other coefficients like ‘gamma’, ‘degree’, ‘coef’ which you can tune in order to reach a best classification.
Learn Data Science by working on interesting Data Science Projects
Example for non-linear classifier
In earlier example we saw the working of SVM algorithm or Maximum margin classifier for a linearly separable data. In the next example we will learn how to classify data if it is not linearly separable. Data: For the exercise we will be using “ESL.Mixture” data provided by Stanford (http://www stat.stanford.edu/~tibs/ElemStatLearn/datasets/ESL.mixture.rda)
You can download the rda file from the website and load the data into R. Below plot is showing how our data looks like, and you can clearly see that there is no clear boundary which can separate the “Red” points from “Black” ones. Hence, Maximum Margin Classifier or Support Vector Classifier can’t be applied in this case-

Let’s try to run SVM algorithm using “Radial” Kernel for our purpose –

The output of print(fit) looks like below –
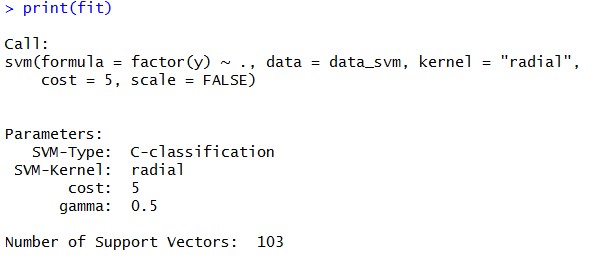
We can see that to classify data or to create decision boundary SVM algorithm has used 103 support vectors. Let’s plot the output of SVM algorithm on ESL.mixture data and see how “Radial” Kernel worked out–

Looks like SVM with “Radial” kernel has done a pretty decent job in classifying our data into given two categories. You can try other available Kernels and play with tuning parameters and see how different Kernels are working out.
Explore More Data Science and Machine Learning Projects for Practice. Fast-Track Your Career Transition with ProjectPro
SVM & Linear Regression
Very few people know that SVM is not only limited to classification but also can be applied to the cases which are supposed to be solved by linear regression. We will use the following data to show that how SVM fits in this application. Here we are trying to predict ‘y’ using values given in ‘x’.
|
x |
y |
|
1 |
2 |
|
2 |
1 |
|
3 |
3 |
|
4 |
6 |
|
5 |
9 |
|
6 |
11 |
|
7 |
13 |
|
8 |
15 |
|
9 |
17 |
|
10 |
20 |

Now, let see how well the predictions are –
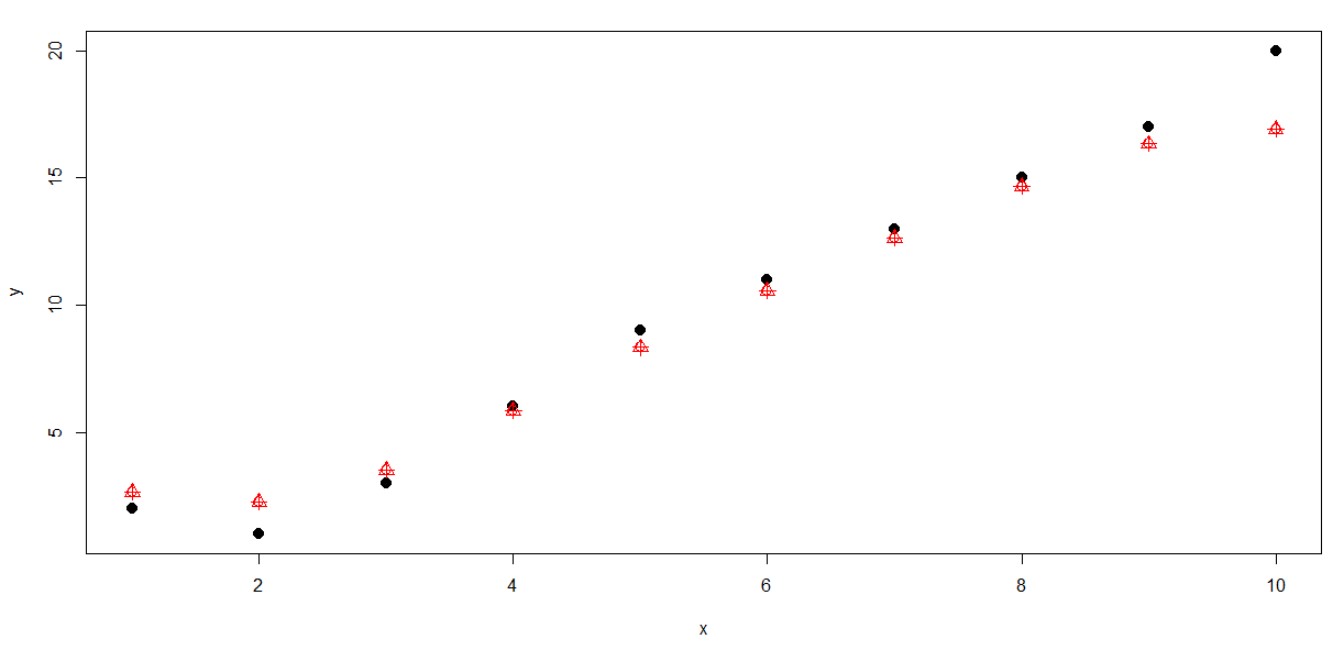
The Back points here represent the actual data while the Red points represent the predicted values fitted by SVM linear regression model. We can see that the predictions are pretty much similar to the actual values.
Recommended Tutorials:
Codes
Example 1: Maximum Margin Classifier
# Creating a dataset to run SVM algorithm
data<-read.csv("D:\\SVM\\data.csv")
plot(data[c(1,2)],col=data$Flag+3,pch=19,cex=1.4)
# Loading library
library(e1071)
# Fitting the data
data$Flag<-as.factor(data$Flag)
svmfit = svm(Flag ~ ., data = data, kernel = "linear",cost=-10)
print(svmfit)
plot(svmfit,data)Example 2: Support Vector Machine (Non Linear Classifier)
# Non - Linear classifier
load('D:\\SVM\\ESL.mixture.rda')
names(ESL.mixture)
plot(ESL.mixture$x,col=ESL.mixture$y+1)
# Let's prepare the data
data_svm <- data.frame(y = factor(ESL.mixture$y), ESL.mixture$x)
# Running the SVM with "Radial" Kernel
fit = svm(factor(y) ~ ., data = data_svm, scale = FALSE,
kernel = "radial", cost = 5)
print(fit)
plot(fit,data_svm)Example 3: Support Vector Machine: Regression
#Reading the data
data<-read.csv("D:\\SVM\\data2.csv")
#Running model
model<-svm(y~x,data)
summary(model)
#Fitting model and predicting results
data$predicted<-predict(model,data)
plot(data[c(1,2)],pch=19,cex=1.4)
points(data$x, data$predicted, col = "red", pch=3,cex=1.4)



